- Home
- Process Worldview
- Community
- Art and Music
- Whitehead and Process Thinking
- Podcasts
- Spirituality
- Ecological Civilization
- Education
- Contact
- Social Justice
- Science
- Animals
- Sacred Poems
- Whitehead Videos
- Index of All Titles
- Practicing Process Thought
- Process Spirituality: A Spiritual Alphabet
- Recent Posts
Five Ideas from David Bohm
as articulated in his "The Implicate or Enfolded Order: A New Order for Physics."
David Bohm believes that quantum theory requires a new understanding of order: an implicate order: "What I want to suggest here is that the quantum theory, understood imaginatively, gives a clear indication that we now need yet further new notions of order, as different perhaps from those of Descartes as these latter are from those prevailing in ancient Greece."
1. A sense of the implicate order invites us to recognize the whole is contained in each part.
"What is important here, however, is not this three-dimensionality but rather that, in some sense, each part of the hologram contains the whole object."
2. A sense of the implicate order also invites us to recognize that each part manifests a still larger and undivided whole from which all things emerge: the holomovement.
"The holomovement is to be understood as necessarily and essentially undivided. The holomovement is to be understood as necessarily and essentially undivided. Since it has no divisions, there can be no explicit way to describe or specify it. It can be known only implicitly, through particular manifestations (such as light, sound, electrons, etc.). Such manifestations have a certain relative autonomy, i.e., self-rule, in their order of movement, and this permits them to be studied in themselves, at least up to a point. But ultimately this autonomy is limited, because the fundamental order is holonomy, i.e., the law of the whole."
3. The parts of a whole can be physical objects or mental events, including creative acts of intelligent perception.
"What all this means is that the flux of the holomovement is the implicate source of all forms, both physical and mental. That is to say, the whole of existence, including inanimate matter, living organisms, and ‘mind,’ arises in a single ground, in which these are all enfolded, or contained implicitly. Inanimate matter is characterized by a relatively autonomous mechanical order of behaviour (i.e., a dominant tendency to recurrence, repetition, relatively fixed and stable patterns of movement, etc.). This order is inherited mainly from the past. On the other hand, what is essential to mind is the possibility of a fresh creative act of intelligent perception, which can assimilate knowledge from the past, but which is not dominated by this knowledge."
4. We humans can perceive the world in this way. We can perceive holistically.
"Similarly, when we look into the depths of the clear sky, what we actually see is an unspecifiable total ground of movement, from which objects emerge. Particular ideas or thoughts coming to the mind may similarly be perceived as being like particular objects that arise from an unspecifiable ground of deeper movement. What we call ‘mind’ may be this deeper ground of movement, but if we think of the particular thoughts as the basic reality, we miss this."
5. The energy of life more closely reveals the innermost order more than inanimate matter. The innermost order is a holomovement. It can be called life energy.
It is clear that, in this view, living organisms are to be regarded as particular manifestations of what is ultimately enfolded in the inward depths of the holomovement. We are suggesting here that a living organism has a more direct contact with what is thus enfolded in the holomovement than does inanimate matter. When such an organism dies, this relatively direct contact ceases to operate, so that the body of the organism reverts back to the more mechanical order of inanimate matter. So, in a certain sense, we could say that the energy of life more typically reveals the innermost order of the holomovement than does inanimate matter. For this reason, one can appropriately call the holomovement the life energy, which is the ground that ultimately creates and sustains all matter and all mind, as two relatively autonomous and independent streams that may move in parallel.
1. A sense of the implicate order invites us to recognize the whole is contained in each part.
"What is important here, however, is not this three-dimensionality but rather that, in some sense, each part of the hologram contains the whole object."
2. A sense of the implicate order also invites us to recognize that each part manifests a still larger and undivided whole from which all things emerge: the holomovement.
"The holomovement is to be understood as necessarily and essentially undivided. The holomovement is to be understood as necessarily and essentially undivided. Since it has no divisions, there can be no explicit way to describe or specify it. It can be known only implicitly, through particular manifestations (such as light, sound, electrons, etc.). Such manifestations have a certain relative autonomy, i.e., self-rule, in their order of movement, and this permits them to be studied in themselves, at least up to a point. But ultimately this autonomy is limited, because the fundamental order is holonomy, i.e., the law of the whole."
3. The parts of a whole can be physical objects or mental events, including creative acts of intelligent perception.
"What all this means is that the flux of the holomovement is the implicate source of all forms, both physical and mental. That is to say, the whole of existence, including inanimate matter, living organisms, and ‘mind,’ arises in a single ground, in which these are all enfolded, or contained implicitly. Inanimate matter is characterized by a relatively autonomous mechanical order of behaviour (i.e., a dominant tendency to recurrence, repetition, relatively fixed and stable patterns of movement, etc.). This order is inherited mainly from the past. On the other hand, what is essential to mind is the possibility of a fresh creative act of intelligent perception, which can assimilate knowledge from the past, but which is not dominated by this knowledge."
4. We humans can perceive the world in this way. We can perceive holistically.
"Similarly, when we look into the depths of the clear sky, what we actually see is an unspecifiable total ground of movement, from which objects emerge. Particular ideas or thoughts coming to the mind may similarly be perceived as being like particular objects that arise from an unspecifiable ground of deeper movement. What we call ‘mind’ may be this deeper ground of movement, but if we think of the particular thoughts as the basic reality, we miss this."
5. The energy of life more closely reveals the innermost order more than inanimate matter. The innermost order is a holomovement. It can be called life energy.
It is clear that, in this view, living organisms are to be regarded as particular manifestations of what is ultimately enfolded in the inward depths of the holomovement. We are suggesting here that a living organism has a more direct contact with what is thus enfolded in the holomovement than does inanimate matter. When such an organism dies, this relatively direct contact ceases to operate, so that the body of the organism reverts back to the more mechanical order of inanimate matter. So, in a certain sense, we could say that the energy of life more typically reveals the innermost order of the holomovement than does inanimate matter. For this reason, one can appropriately call the holomovement the life energy, which is the ground that ultimately creates and sustains all matter and all mind, as two relatively autonomous and independent streams that may move in parallel.
The Implicate or Enfolded Order:
A New Order for Physics
by David Bohm
from Mind in Nature: The Interface of Science and Philosophy
by John B. Cobb and David Ray Griffin *
reposted with permission from Religion Online
scroll down for diagrams
Diagram 1Diagram 2Diagram 3Diagram 4 |
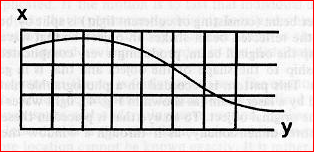
The quantum theory is, without doubt, the most revolutionary development in modern physics. Unfortunately, a large part of its potential impact on our overall world view has been lost sight of, because it is generally treated as being nothing more than a calculus, for which no general imaginative conception is thought to be possible. The main emphasis in working with this theory has therefore been on the development of a mathematical formalism that can predict the widest possible range of experimental results. In this talk I shall, however, describe in general terms how the quantum theory, understood somewhat more imaginatively than is usually done, can point to a new order in physics, which I call the enfolded order, or the implicate order. I shall begin by sketching briefly a few salient historical features in the development of our modern notions of order in physics. Now, the ancient Greeks thought in terms of an essential order of aesthetic and moral perfection, which is least on the surface of the Earth and increases progressively toward the Heavens. And so, they were led to suppose that Heavenly bodies should express the perfection of their nature by moving in what they thought to be the most perfect of geometrical figures -- the circle. When observations failed to disclose such circular orbits, they retained their notions of essential order by supposing that the movements could be analyzed in terms of the Ptolemaic epicycles, i.e., circles on top of circles. In more modern times, as is well known, this view was overturned by the Copernican idea that the Sun is at the centre (and ultimately that there is no determinate centre at all). This idea led to the development of an entirely new notion of essential order, which was expressed in terms of a detailed description of the mechanical motions of bodies through space. This order was first given a precise mathematical form by Descartes, through his invention of co-ordinates. The co-ordinates are pictured with the aid of a grid (as shown in Fig. 1). |
The orbit of a body is described by a curve, given algebraically by an equation determining a ‘coordination’ between two orders, that of the position, x, and that of the time, t.
Clearly, the Cartesian co-ordinates constitute a way of thinking of order that is radically different from that of the ancient Greeks. These co-ordinates have entered the whole of physics and are by now pervasively present in almost all that physicists do. In fact, it can safely be said that, while almost all the detailed content of physical thinking has changed fundamentally in the past few hundred years, the idea of co-ordinates is the one thing that has remained essentially constant. And this need not be felt to be surprising, if one takes into account that basic notions of order tend to be among the most strongly retained features of our thinking.
What I want to suggest here is that the quantum theory, understood imaginatively, gives a clear indication that we now need yet further new notions of order, as different perhaps from those of Descartes as these latter are from those prevailing in ancient Greece. I can give here only a brief description indicating certain essential features of my proposals concerning these new notions of order (which have been discussed in more detail elsewhere). In doing this, I shall use the hologram as an illustrative example, with the aid of which we can consider these notions not only mathematically, but also imaginatively.
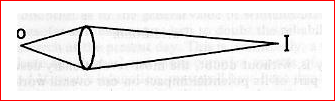
Now, traditionally, the world was thought to be constituted of points. This view was given a great deal of support through the use of the lens, which provides in principle (as shown in Fig. 2) a point-to-point correspondence between object, O, and Image, I. By creating such a correspondence, the lens brings the concept of point out in our minds in sharp relief, and encourages us to suppose that ultimately the whole of reality can be analyzed in terms of points which are to be regarded as, in some basic sense, separately existent.
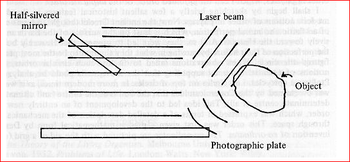
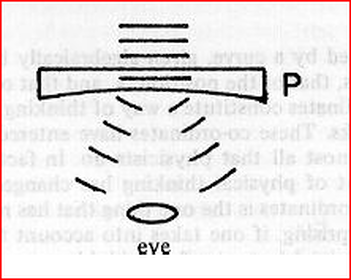
The hologram, however, works in a very different way. To show this difference, we consider the diagram in Fig. 3. A laser beam (consisting of coherent light) is split by being passed through a half silvered mirror. Part of the reflected beam strikes an object, so that waves from this object diffract and come back to overlap the original beam, producing a very complicated interference pattern that has no obvious relationship to the shape of the object and that is in general too fine even to be visible to the naked eye. This pattern is recorded on a photographic plate. When a section of this same plate is illuminated by a laser beam (as shown in Fig. 4), light waves come out which are similar to those coming from the original object. To an eye that is placed in these waves, it appears that the original object is seen three-dimensionally, as if through a window the size of a beam. What is important here, however, is not this three-dimensionality but rather that, in some sense, each part of the hologram contains the whole object.
This example indicates a new order not hitherto given serious attention in physics. Actually, of course, the photographic plate is merely a convenient way of recording this order. Primarily, however, the order is in the movement of the light whose intensity is recorded. What is characteristic of this order is that a whole is enfolded in the movement in each region of space. This movement may appear at first sight to be more or less random, but evidently it has a complex order within it. This we call the implicate order.
Cartesian co-ordinates, then, express the unfolded or explicate order, in which the analysis of everything into separate points has been the general means of understanding the world. In physics, the explicate order has until now been considered to be fundamental for expressing the laws of nature. Thus, Newton’s laws of motion are a relationship determining an unfolded order of successive positions occupied by an object at a series of successive times. What I am proposing here, however, is that the quantum theory indicates the need to take the implicate order as fundamental. In other words, the essential order of movement is not that of an object translating itself from one place to another, but rather, it is a folding and unfolding, in which the object is continually being created again, in a form generally similar to what it was, though different in detail. The explicate order of movement of the object is thus not independent, substantial, and self-existent. We suggest instead that it is an appearance, abstracted from the implicate order, on which it depends and from which it derives its whole form and set of characteristic relationships.
The above notion can be brought out by considering an example, in which an insoluble ink droplet is placed inside a viscous fluid, such as glycerine. If the fluid is stirred slowly by a mechanical device (so that there is no diffusion) the droplet is eventually drawn into a fine thread that is distributed throughout the whole system in such a way that it is no longer even visible to the eye. If the mechanical device is then reversed, the thread will slowly gather together until it suddenly coalesces once again into a visible droplet.
Now, before this coalescence took place, the droplet could be said to be ‘folded into’ the viscous fluid, while afterwards it is unfolded again. So we have an example of a movement in which an explicate order is implicated and then explicated.
We may further develop this example by considering a case in which a droplet is first put into the fluid, after which the system is stirred n times. Another droplet is then placed in the fluid at a slightly different position and the system is once again stirred n times. If this operation is given an m-fold repetition, we will end up with a distribution in which the last droplet has been stirred n times. The whole distribution can then be unstirred continuously and one droplet after another will be explicated. If the motion is so fast that individual droplets are not resolved in our perception, it will appear that a permanently existing localized object is continuously moving across the space occupied by the fluid. Actually, however, there is clearly no such object. What underlies this appearance is indeed an implicated order in the distribution of ink throughout the whole system.
The analogy with the quantum theory is fairly easy to see. The quantum theory indicates that at a deep level matter can be understood neither as constituted of localized particles nor as constituted of fields extended through space and undergoing wave motion. Rather, it seems to have some of the attributes of both. Indeed, this is the essential meaning of the uncertainty principle. It is not that particles exist, whose location cannot be known exactly. It is rather that there are no particles, in the sense that the order implicit in the particle model is simply not applicable at this level. But likewise, there are no fields, in the sense that the order implicit in the continuous field model is also not applicable. Some fundamentally new notion of order is therefore needed.
What I am suggesting here is that the notion of implicate order imaginatively captures the essence of this new situation in physics and that it may perhaps serve as a germ for further development of ideas in this domain. Thus, in the example of a series of ink droplets folded into a viscous fluid, we have a movement in which the results visible in certain regions (e.g., ink droplets) originate in and depend on the whole fluid in an inseparable way. The particle-like aspect is evidently implicit or enfolded in this whole. Likewise, this whole has enfolded within it a certain field-like aspect, as demonstrated by the fact that the order of appearance of the enfolded ink droplets may be radically altered by changing the general conditions throughout the whole fluid, e.g., by introducing structures of slits and obstacles within it. (The analogy with the quantum-mechanical inseparability of the results of observation from the overall experimental arrangement is evident here.)
Of course, in the above example one may, if one wishes, explain the implicate order as the result of a distribution of the particles of ink, which can ultimately be understood in terms of the ordinary explicate order of space and time. So, this example, like all analogies, can be used only in some limited sense, as a pointer. We have, therefore, now to return to the hologram, for which no such ultimate analysis in terms of a distribution of localized particles of matter is possible.
Now, with the hologram, light is taken as the particular movement that is involved in the folding and unfolding of a certain structure (e.g., an object). But more generally, it may be sound, electron beams, or any other movement, which like light is able to carry a whole content in each region or part. The totality of all such possibilities, known and unknown, I shall call the holomovement.
The holomovement is to be understood as necessarily and essentially undivided. Since it has no divisions, there can be no explicit way to describe or specify it. It can be known only implicitly, through particular manifestations (such as light, sound, electrons, etc.). Such manifestations have a certain relative autonomy, i.e., self-rule, in their order of movement, and this permits them to be studied in themselves, at least up to a point. But ultimately this autonomy is limited, because the fundamental order is holonomy, i.e., the law of the whole. This law of the whole is, however, just such as to provide for the above described relative and limited autonomy of the partial aspects. This provision for such relative and limited autonomy is indeed a key requirement in any theory which takes the whole as primary, since without it there is no way to understand or even account for the fact that partial aspects can be found which may serve as points of departure in the development of knowledge.
What we are suggesting then is that all matter is to be understood as a relatively autonomous and constant set of forms built on and carried by the universal and indivisible flux of the holomovement. Such material forms have a certain subsistence, in the sense that under appropriate conditions they can continue with a certain limited possibility for stable existence. However, they are not to be regarded as substances, which would be completely stable, permanent and not dependent on something deeper for their continued existence. So the flux of the holomovement, with its implicate order, is the primary reality, while the explicate order of relatively constant material forms is secondary.
It is important to emphasize here that what counts in any theory that is developed along such lines is relative degree of implication. For example, if we take our own order of perceptual experience as explicate, then the electron’s order is implicate. But we might equally well take the electron’s order as explicate, in which case our own experiential order will be implicate. In other words, the laws of nature will be invariant, in the sense that their content will be the same, regardless of which order is taken as explicate. This brings out in another way how the explicate order is an abstraction from the implicate, having no independence or substantiality of existence.
This means, however, that ‘localization’ cannot be a fundamental notion. What is ‘local’ in one order is enfolded throughout the whole of space (and time) in another order. And as pointed out above, any one order is no more fundamental than any other. Space and time are thus an abstraction from the universal flux of process.
This abstraction has ultimately to be expressed precisely in some mathematical form that will give us a new description of implicate order, which is as systematic and coherent as that given in classical physics by the Cartesian co-ordinates.
With the aid of such a mathematical development we then have, of course, to understand the overall situation in physics in a way that is free of current contradictions and confusions (e.g., the infinities of quantum field theory). Work on this is now going on and some progress has been made which will be reported later.
It is also necessary, however, to go much deeper and to explore what the implicate order means with regard to our common-sense notions based on general experience, as well as with regard to our basic philosophical ideas. In short, we have to come to a new general world view, or metaphysics, in which the implicate order is primary, while the explicate order is secondary or derivative.
In developing such a view, we cannot stop with the attempt to understand matter alone through the implicate order. For we ourselves, along with electrons, protons, rocks, planets, galaxies, etc. are only relatively stable forms in the holomovement. It is necessary, moreover, to include not only our bodies, with their brains and nervous systems, but also our thoughts, feelings, urges, will and desire, which are inseparable from the functions of these brains and nervous systems. If the ultimate ground of all matter is in the implicate order, as contained in the holomovement, it thus seems inevitable that what has generally been called ‘mind’ must also have the same ultimate ground.
What we are proposing then is that what can be touched, seen, handled by scientific instruments, etc. is an explicate abstraction from the real implicate totality of the holomovement. Likewise, in physics, the modern quantum mechanical field theory regards ‘particles,’ along with all structures constituted out of them (i.e., material bodies), as small modifications of the ‘vacuum’ (which is, in effect, being treated as an unknown and only implicitly specifiable movement that is the ground of the whole of reality).
Similarly, when we look into the depths of the clear sky, what we actually see is an unspecifiable total ground of movement, from which objects emerge. Particular ideas or thoughts coming to the mind may similarly be perceived as being like particular objects that arise from an unspecifiable ground of deeper movement. What we call ‘mind’ may be this deeper ground of movement, but if we think of the particular thoughts as the basic reality, we miss this.
Such a way of looking at everything fits in rather well with our general experience. Thus, while any statement may give an explicit expression to our thoughts and feelings, the meaning or significance of this statement is in a vast and unspecifiable implicit background of response. Unless we share most of this implicit background, the explicit statement will communicate little or nothing. So one may propose that, also in the mind, the explicate order arises out of the implicate, and that the basic movement is one in which the content of each of these continually passes into the other.
What all this means is that the flux of the holomovement is the implicate source of all forms, both physical and mental. That is to say, the whole of existence, including inanimate matter, living organisms, and ‘mind,’ arises in a single ground, in which these are all enfolded, or contained implicitly. Inanimate matter is characterized by a relatively autonomous mechanical order of behaviour (i.e., a dominant tendency to recurrence, repetition, relatively fixed and stable patterns of movement, etc.). This order is inherited mainly from the past. On the other hand, what is essential to mind is the possibility of a fresh creative act of intelligent perception, which can assimilate knowledge from the past, but which is not dominated by this knowledge. Of course, inanimate matter has certain creative possibilities also, but these evolve relatively slowly. And while mind too can function mechanically and repetitively, this is not its essential quality. Mind, which is deeply creative and new in its essential mode of operation, cannot then be explained in terms of any mechanical abstraction of the properties of inanimate matter. Rather, it is being proposed here that its operation originates in implicate depths of the holomovement beyond those needed for understanding the ordinary mechanical qualities of matter.
It is clear that, in this view, living organisms are to be regarded as particular manifestations of what is ultimately enfolded in the inward depths of the holomovement. We are suggesting here that a living organism has a more direct contact with what is thus enfolded in the holomovement than does inanimate matter. When such an organism dies, this relatively direct contact ceases to operate, so that the body of the organism reverts back to the more mechanical order of inanimate matter. So, in a certain sense, we could say that the energy of life more typically reveals the innermost order of the holomovement than does inanimate matter. For this reason, one can appropriately call the holomovement the life energy, which is the ground that ultimately creates and sustains all matter and all mind, as two relatively autonomous and independent streams that may move in parallel.
This view does not deny the importance of the mechanical abstraction of the structure of the living organism. But it denies that the abstraction of mechanism comprehends the ultimate ground of life, and indeed it denies also that such an abstraction comprehends the ultimate ground of inanimate matter. Nor are we saying (e.g., with Descartes) that mind and matter are to be considered as two independently existent substances. Rather, the universal life energy is what operates in the role that has generally been attributed to the one self-existent substance, which is the implicate ground of every form that comes to explicate manifestation.
The view outlined above is evidently close, in important respects, to that of Spinoza. The main difference is perhaps that the notion of implicate order may be more suitable for accomplishing what Spinoza intended, than was the logical geometrical form that he used. For example, the modes and aspects that he introduced to describe the activity of substance can be understood as relatively autonomous orders of movement. A key point introduced by the notion of implicate order is that it is not possible in general for all such modes to be explicate together. Rather (as indicated by the fact that different quantum mechanical ‘observables’ cannot generally be defined simultaneously), when one mode is explicate, others will have to be implicate.
One can in this general way regard the implicate order as a further development of what is already present in Spinoza, as well as in Heraclitus, Cusano, Leibniz, Whitehead and others, a development that is capable of making full contact with modern science, and yet opens up a way to assimilate common experience and general philosophical reflections on this experience, to give a single, whole, unfragmented world view.
* Published by University Press of America, 1977. This book was prepared for Religion Online by Ted and Winnie Brock. Religion Online is designed to assist teachers, scholars and general “seekers” who are interested in exploring religious issues. Its aim is to develop an extensive library of resources, representing many different points of view, but all written from the perspective of sound scholarship.
Clearly, the Cartesian co-ordinates constitute a way of thinking of order that is radically different from that of the ancient Greeks. These co-ordinates have entered the whole of physics and are by now pervasively present in almost all that physicists do. In fact, it can safely be said that, while almost all the detailed content of physical thinking has changed fundamentally in the past few hundred years, the idea of co-ordinates is the one thing that has remained essentially constant. And this need not be felt to be surprising, if one takes into account that basic notions of order tend to be among the most strongly retained features of our thinking.
What I want to suggest here is that the quantum theory, understood imaginatively, gives a clear indication that we now need yet further new notions of order, as different perhaps from those of Descartes as these latter are from those prevailing in ancient Greece. I can give here only a brief description indicating certain essential features of my proposals concerning these new notions of order (which have been discussed in more detail elsewhere). In doing this, I shall use the hologram as an illustrative example, with the aid of which we can consider these notions not only mathematically, but also imaginatively.
Now, traditionally, the world was thought to be constituted of points. This view was given a great deal of support through the use of the lens, which provides in principle (as shown in Fig. 2) a point-to-point correspondence between object, O, and Image, I. By creating such a correspondence, the lens brings the concept of point out in our minds in sharp relief, and encourages us to suppose that ultimately the whole of reality can be analyzed in terms of points which are to be regarded as, in some basic sense, separately existent.
The hologram, however, works in a very different way. To show this difference, we consider the diagram in Fig. 3. A laser beam (consisting of coherent light) is split by being passed through a half silvered mirror. Part of the reflected beam strikes an object, so that waves from this object diffract and come back to overlap the original beam, producing a very complicated interference pattern that has no obvious relationship to the shape of the object and that is in general too fine even to be visible to the naked eye. This pattern is recorded on a photographic plate. When a section of this same plate is illuminated by a laser beam (as shown in Fig. 4), light waves come out which are similar to those coming from the original object. To an eye that is placed in these waves, it appears that the original object is seen three-dimensionally, as if through a window the size of a beam. What is important here, however, is not this three-dimensionality but rather that, in some sense, each part of the hologram contains the whole object.
This example indicates a new order not hitherto given serious attention in physics. Actually, of course, the photographic plate is merely a convenient way of recording this order. Primarily, however, the order is in the movement of the light whose intensity is recorded. What is characteristic of this order is that a whole is enfolded in the movement in each region of space. This movement may appear at first sight to be more or less random, but evidently it has a complex order within it. This we call the implicate order.
Cartesian co-ordinates, then, express the unfolded or explicate order, in which the analysis of everything into separate points has been the general means of understanding the world. In physics, the explicate order has until now been considered to be fundamental for expressing the laws of nature. Thus, Newton’s laws of motion are a relationship determining an unfolded order of successive positions occupied by an object at a series of successive times. What I am proposing here, however, is that the quantum theory indicates the need to take the implicate order as fundamental. In other words, the essential order of movement is not that of an object translating itself from one place to another, but rather, it is a folding and unfolding, in which the object is continually being created again, in a form generally similar to what it was, though different in detail. The explicate order of movement of the object is thus not independent, substantial, and self-existent. We suggest instead that it is an appearance, abstracted from the implicate order, on which it depends and from which it derives its whole form and set of characteristic relationships.
The above notion can be brought out by considering an example, in which an insoluble ink droplet is placed inside a viscous fluid, such as glycerine. If the fluid is stirred slowly by a mechanical device (so that there is no diffusion) the droplet is eventually drawn into a fine thread that is distributed throughout the whole system in such a way that it is no longer even visible to the eye. If the mechanical device is then reversed, the thread will slowly gather together until it suddenly coalesces once again into a visible droplet.
Now, before this coalescence took place, the droplet could be said to be ‘folded into’ the viscous fluid, while afterwards it is unfolded again. So we have an example of a movement in which an explicate order is implicated and then explicated.
We may further develop this example by considering a case in which a droplet is first put into the fluid, after which the system is stirred n times. Another droplet is then placed in the fluid at a slightly different position and the system is once again stirred n times. If this operation is given an m-fold repetition, we will end up with a distribution in which the last droplet has been stirred n times. The whole distribution can then be unstirred continuously and one droplet after another will be explicated. If the motion is so fast that individual droplets are not resolved in our perception, it will appear that a permanently existing localized object is continuously moving across the space occupied by the fluid. Actually, however, there is clearly no such object. What underlies this appearance is indeed an implicated order in the distribution of ink throughout the whole system.
The analogy with the quantum theory is fairly easy to see. The quantum theory indicates that at a deep level matter can be understood neither as constituted of localized particles nor as constituted of fields extended through space and undergoing wave motion. Rather, it seems to have some of the attributes of both. Indeed, this is the essential meaning of the uncertainty principle. It is not that particles exist, whose location cannot be known exactly. It is rather that there are no particles, in the sense that the order implicit in the particle model is simply not applicable at this level. But likewise, there are no fields, in the sense that the order implicit in the continuous field model is also not applicable. Some fundamentally new notion of order is therefore needed.
What I am suggesting here is that the notion of implicate order imaginatively captures the essence of this new situation in physics and that it may perhaps serve as a germ for further development of ideas in this domain. Thus, in the example of a series of ink droplets folded into a viscous fluid, we have a movement in which the results visible in certain regions (e.g., ink droplets) originate in and depend on the whole fluid in an inseparable way. The particle-like aspect is evidently implicit or enfolded in this whole. Likewise, this whole has enfolded within it a certain field-like aspect, as demonstrated by the fact that the order of appearance of the enfolded ink droplets may be radically altered by changing the general conditions throughout the whole fluid, e.g., by introducing structures of slits and obstacles within it. (The analogy with the quantum-mechanical inseparability of the results of observation from the overall experimental arrangement is evident here.)
Of course, in the above example one may, if one wishes, explain the implicate order as the result of a distribution of the particles of ink, which can ultimately be understood in terms of the ordinary explicate order of space and time. So, this example, like all analogies, can be used only in some limited sense, as a pointer. We have, therefore, now to return to the hologram, for which no such ultimate analysis in terms of a distribution of localized particles of matter is possible.
Now, with the hologram, light is taken as the particular movement that is involved in the folding and unfolding of a certain structure (e.g., an object). But more generally, it may be sound, electron beams, or any other movement, which like light is able to carry a whole content in each region or part. The totality of all such possibilities, known and unknown, I shall call the holomovement.
The holomovement is to be understood as necessarily and essentially undivided. Since it has no divisions, there can be no explicit way to describe or specify it. It can be known only implicitly, through particular manifestations (such as light, sound, electrons, etc.). Such manifestations have a certain relative autonomy, i.e., self-rule, in their order of movement, and this permits them to be studied in themselves, at least up to a point. But ultimately this autonomy is limited, because the fundamental order is holonomy, i.e., the law of the whole. This law of the whole is, however, just such as to provide for the above described relative and limited autonomy of the partial aspects. This provision for such relative and limited autonomy is indeed a key requirement in any theory which takes the whole as primary, since without it there is no way to understand or even account for the fact that partial aspects can be found which may serve as points of departure in the development of knowledge.
What we are suggesting then is that all matter is to be understood as a relatively autonomous and constant set of forms built on and carried by the universal and indivisible flux of the holomovement. Such material forms have a certain subsistence, in the sense that under appropriate conditions they can continue with a certain limited possibility for stable existence. However, they are not to be regarded as substances, which would be completely stable, permanent and not dependent on something deeper for their continued existence. So the flux of the holomovement, with its implicate order, is the primary reality, while the explicate order of relatively constant material forms is secondary.
It is important to emphasize here that what counts in any theory that is developed along such lines is relative degree of implication. For example, if we take our own order of perceptual experience as explicate, then the electron’s order is implicate. But we might equally well take the electron’s order as explicate, in which case our own experiential order will be implicate. In other words, the laws of nature will be invariant, in the sense that their content will be the same, regardless of which order is taken as explicate. This brings out in another way how the explicate order is an abstraction from the implicate, having no independence or substantiality of existence.
This means, however, that ‘localization’ cannot be a fundamental notion. What is ‘local’ in one order is enfolded throughout the whole of space (and time) in another order. And as pointed out above, any one order is no more fundamental than any other. Space and time are thus an abstraction from the universal flux of process.
This abstraction has ultimately to be expressed precisely in some mathematical form that will give us a new description of implicate order, which is as systematic and coherent as that given in classical physics by the Cartesian co-ordinates.
With the aid of such a mathematical development we then have, of course, to understand the overall situation in physics in a way that is free of current contradictions and confusions (e.g., the infinities of quantum field theory). Work on this is now going on and some progress has been made which will be reported later.
It is also necessary, however, to go much deeper and to explore what the implicate order means with regard to our common-sense notions based on general experience, as well as with regard to our basic philosophical ideas. In short, we have to come to a new general world view, or metaphysics, in which the implicate order is primary, while the explicate order is secondary or derivative.
In developing such a view, we cannot stop with the attempt to understand matter alone through the implicate order. For we ourselves, along with electrons, protons, rocks, planets, galaxies, etc. are only relatively stable forms in the holomovement. It is necessary, moreover, to include not only our bodies, with their brains and nervous systems, but also our thoughts, feelings, urges, will and desire, which are inseparable from the functions of these brains and nervous systems. If the ultimate ground of all matter is in the implicate order, as contained in the holomovement, it thus seems inevitable that what has generally been called ‘mind’ must also have the same ultimate ground.
What we are proposing then is that what can be touched, seen, handled by scientific instruments, etc. is an explicate abstraction from the real implicate totality of the holomovement. Likewise, in physics, the modern quantum mechanical field theory regards ‘particles,’ along with all structures constituted out of them (i.e., material bodies), as small modifications of the ‘vacuum’ (which is, in effect, being treated as an unknown and only implicitly specifiable movement that is the ground of the whole of reality).
Similarly, when we look into the depths of the clear sky, what we actually see is an unspecifiable total ground of movement, from which objects emerge. Particular ideas or thoughts coming to the mind may similarly be perceived as being like particular objects that arise from an unspecifiable ground of deeper movement. What we call ‘mind’ may be this deeper ground of movement, but if we think of the particular thoughts as the basic reality, we miss this.
Such a way of looking at everything fits in rather well with our general experience. Thus, while any statement may give an explicit expression to our thoughts and feelings, the meaning or significance of this statement is in a vast and unspecifiable implicit background of response. Unless we share most of this implicit background, the explicit statement will communicate little or nothing. So one may propose that, also in the mind, the explicate order arises out of the implicate, and that the basic movement is one in which the content of each of these continually passes into the other.
What all this means is that the flux of the holomovement is the implicate source of all forms, both physical and mental. That is to say, the whole of existence, including inanimate matter, living organisms, and ‘mind,’ arises in a single ground, in which these are all enfolded, or contained implicitly. Inanimate matter is characterized by a relatively autonomous mechanical order of behaviour (i.e., a dominant tendency to recurrence, repetition, relatively fixed and stable patterns of movement, etc.). This order is inherited mainly from the past. On the other hand, what is essential to mind is the possibility of a fresh creative act of intelligent perception, which can assimilate knowledge from the past, but which is not dominated by this knowledge. Of course, inanimate matter has certain creative possibilities also, but these evolve relatively slowly. And while mind too can function mechanically and repetitively, this is not its essential quality. Mind, which is deeply creative and new in its essential mode of operation, cannot then be explained in terms of any mechanical abstraction of the properties of inanimate matter. Rather, it is being proposed here that its operation originates in implicate depths of the holomovement beyond those needed for understanding the ordinary mechanical qualities of matter.
It is clear that, in this view, living organisms are to be regarded as particular manifestations of what is ultimately enfolded in the inward depths of the holomovement. We are suggesting here that a living organism has a more direct contact with what is thus enfolded in the holomovement than does inanimate matter. When such an organism dies, this relatively direct contact ceases to operate, so that the body of the organism reverts back to the more mechanical order of inanimate matter. So, in a certain sense, we could say that the energy of life more typically reveals the innermost order of the holomovement than does inanimate matter. For this reason, one can appropriately call the holomovement the life energy, which is the ground that ultimately creates and sustains all matter and all mind, as two relatively autonomous and independent streams that may move in parallel.
This view does not deny the importance of the mechanical abstraction of the structure of the living organism. But it denies that the abstraction of mechanism comprehends the ultimate ground of life, and indeed it denies also that such an abstraction comprehends the ultimate ground of inanimate matter. Nor are we saying (e.g., with Descartes) that mind and matter are to be considered as two independently existent substances. Rather, the universal life energy is what operates in the role that has generally been attributed to the one self-existent substance, which is the implicate ground of every form that comes to explicate manifestation.
The view outlined above is evidently close, in important respects, to that of Spinoza. The main difference is perhaps that the notion of implicate order may be more suitable for accomplishing what Spinoza intended, than was the logical geometrical form that he used. For example, the modes and aspects that he introduced to describe the activity of substance can be understood as relatively autonomous orders of movement. A key point introduced by the notion of implicate order is that it is not possible in general for all such modes to be explicate together. Rather (as indicated by the fact that different quantum mechanical ‘observables’ cannot generally be defined simultaneously), when one mode is explicate, others will have to be implicate.
One can in this general way regard the implicate order as a further development of what is already present in Spinoza, as well as in Heraclitus, Cusano, Leibniz, Whitehead and others, a development that is capable of making full contact with modern science, and yet opens up a way to assimilate common experience and general philosophical reflections on this experience, to give a single, whole, unfragmented world view.
* Published by University Press of America, 1977. This book was prepared for Religion Online by Ted and Winnie Brock. Religion Online is designed to assist teachers, scholars and general “seekers” who are interested in exploring religious issues. Its aim is to develop an extensive library of resources, representing many different points of view, but all written from the perspective of sound scholarship.
Wholeness as Beauty
Addendum: A Short Note
on Process and Wholeness
Wholeness is always in process. This is true of personal wholeness, community wholeness, planetary wholeness, and holistic thinking. No form of wholeness is fixed or settled, static or stagnant. And no form is permanent. Even the divine whole, even God, is a whole in process.
Indeed, perhaps with the exception of divine wholeness, wholeness is unstable. It can come and then pass away. And even in its unstable forms, wholeness comes by degree. A person, a community, a planet can be whole in some ways, but not in others. And a whole can be relatively whole, but not completely whole. For human beings, complete wholeness will have to wait for heaven, whether it be a beatific vision or an everlasting communion or a dropping away of individual selfhood into the deep nothing.
Still, wholeness is well worth seeking, Whitehead puts it this way in Process and Reality, wholeness is the satisfying intensity that is felt by a concrescing subject in a moment of concresence as that subject weaves together influences from the past actual world into a gestalt, a whole. Wholeness is a moment of beauty.
What is important in human life is to recognize that different beings have and enjoy different kinds of wholeness. Bacteria and living cells, plants and animals, infants and adults - all aim toward and enjoy some kind of wholeness. The need in our time is to think holistically in ways that incline our hearts and minds toward a recognition and appreciation of the many kinds of wholeness. David Bohm offers one kind of holistic thinking by encouraging us to think of the order of the universe itself as a journey toward and in wholeness.
Indeed, perhaps with the exception of divine wholeness, wholeness is unstable. It can come and then pass away. And even in its unstable forms, wholeness comes by degree. A person, a community, a planet can be whole in some ways, but not in others. And a whole can be relatively whole, but not completely whole. For human beings, complete wholeness will have to wait for heaven, whether it be a beatific vision or an everlasting communion or a dropping away of individual selfhood into the deep nothing.
Still, wholeness is well worth seeking, Whitehead puts it this way in Process and Reality, wholeness is the satisfying intensity that is felt by a concrescing subject in a moment of concresence as that subject weaves together influences from the past actual world into a gestalt, a whole. Wholeness is a moment of beauty.
What is important in human life is to recognize that different beings have and enjoy different kinds of wholeness. Bacteria and living cells, plants and animals, infants and adults - all aim toward and enjoy some kind of wholeness. The need in our time is to think holistically in ways that incline our hearts and minds toward a recognition and appreciation of the many kinds of wholeness. David Bohm offers one kind of holistic thinking by encouraging us to think of the order of the universe itself as a journey toward and in wholeness.